随机(Randomness)指在已知信息中,某些事物缺乏明确的模式或可预测性。它们通常没有顺序,也不遵循可理解的模式或组合。随机意味着不确定性、多结果。
之所以“随机”(或者说不确定),是由于诸多偶然因素(或主观或客观)同时作用所导致的,这些原因所造成的影响往往不是单纯地加法或者乘法,我们无法将它们一一分离开来。
长期以来,人们总是想对不确定性问题给予一个确定性的度量,以展示他们对不确定性问题的信念程度,然后说服其他人对于不确定性问题的看法。
概率(Probability)是对随机现象的不确定性的一种度量,体现了事物发展的某种趋势,概率模型是对随机现象的数学描述。
随机事件与概率
随机现象
在一定的条件下,并不总是出现相同结果的现象称为随机现象(Random phenomenon);只存在一个结果的现象称为确定性现象(Deterministic phenomenon);对在相同的条件下,以重复的随机现象的观察、记录和实验的研究称为随机试验(Random experiment)1。慨率论与数理统计主要研究能大量重复的随机现象和随机试验,但也十分注意研究不能重复的随机现象。
例如:
- 在某款格斗游戏中,根据游戏的设计,玩家每次受到的伤害不总是相同的,这就属于随机现象;
- 太阳每天都会东升西降,这就属于确定性现象;
- 在工厂中,工程师需要估计某个零件的性能,经过了上千次的实验,这就属于随机试验。
对于随机现象通常关心的是在试验或观察中某个结果是否出现,我们称这些结果为随机事件。
单个随机事件是不可预测的,具有偶然性。但如果存在已知的概率分布(即将概率以某种方式分配给不同的结果),则重复事件(试验)中不同结果的频率是可预测的。
样本空间与随机事件
要使得概率论有意义,必须明确所探讨的问题的可能结果究竟是什么。样本点是抽样(Sample)的最基本单元,认识随机现象首先要列出它的样本空间。
样本空间和样本点
随机现象的一切可能基本结果组成的集合称为样本空间(Sample space),记为 ${\mit\Omega}=\{\omega\}$,其中 $\omega$ 表示基本结果,称为样本点(Sample point)。
样本空间是一个关于试验或者观察的理想化模型。
样本点的性质与数学定义是无关的,样本空间(及其定义在样本空间上的概率分布)决定了理想的试验。一个样本空间就是一个概率数学模型,同一个样本空间可以允许有多种不同的实际解释。比如一个样本空间为 $\mathbb{Z}^{+}$,它既可以解释为一本书存在的错字个数,也可以解释为商店一天的到店顾客人数。
将样本点的个数为有限个或可列的情况归为一类,称为离散样本空间(Discrete sample space);而将样本点的个数为不可列无限个的情况归为另一类,称为连续样本空间(Continuous sample space)。
下面的例子分别解释了何为离散样本空间和连续样本空间:
- 在研究英文字母的使用情况时,可能出现的结果为 $A,B,\cdots,Z$ 和空格“$\text{␣}$”,将样本空间选定为 ${\mit\Omega}=\{\text{␣}, A,B,\cdots,Z\}$ 是合适的,它是一个离散的样本空间;
- 用 $t$ 表示用户在某 App 上使用的时间,那么“用户使用时间”的样本空间就是所有非负实数 ${\mit\Omega}=\{t\mid t\geqslant0\}$,它是一个连续的样本空间。
在确定样本空间的时候,不同的试验结果必须是相互排斥的,即在试验过程中只能产生唯一的一个结果。需要注意的是随机现象的样本空间要包含至少两个样本点。若将确定性现象也一并考虑,那么仅含有一个样本点的样本空间,所对应的确定性现象。
随机事件
样本空间的一个子集称作随机事件,简称事件(Event),通常用大写的英文字母 $A,B,C,\cdots$ 表示。
例如掷骰子所出现点数的样本空间为 ${\mit\Omega}=\{1,2,3,4,5,6\}$,那么可以定义集合 $\{1,3,5\}$ 为事件“掷到奇数点”,也可以定义集合 $\{4,5,6\}$ 为事件“掷到的点数大于 3”……
由样本空间 $\mit\Omega$ 中的单个元素组成的子集称为基本事件(Elementary event),而样本空间 $\mit\Omega$ 的最大子集(即 $\mit\Omega$ 本身)称为必然事件(Certain event),样本空间 $\mit\Omega$ 的最小子集(即空集 $\varnothing$)称为不可能事件(Impossible event)。
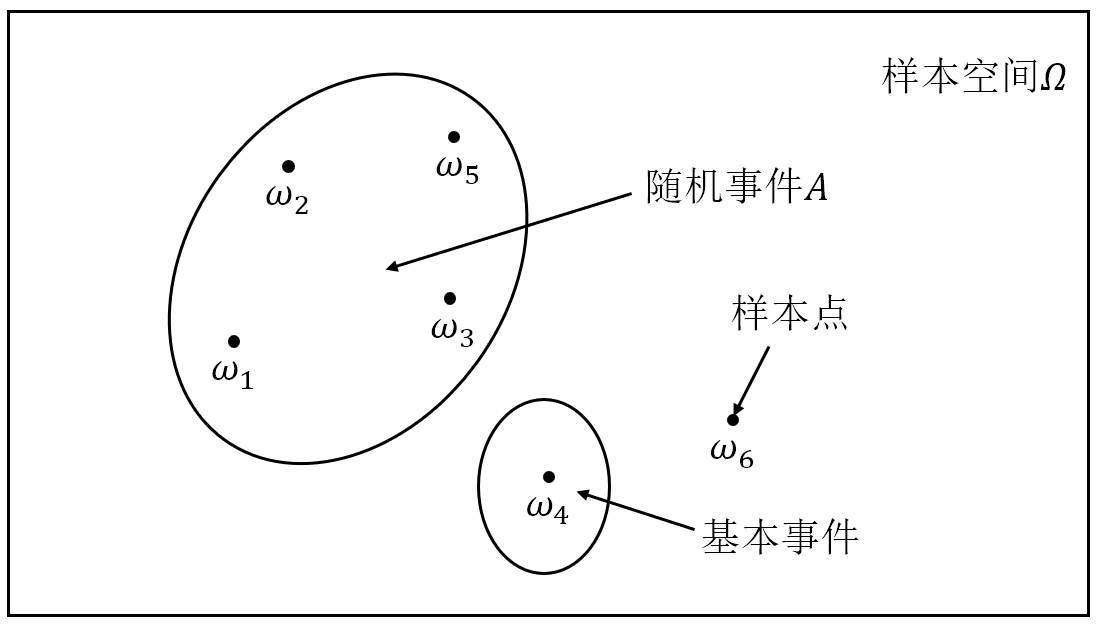
图 1: 样本空间、样本点与随机事件
基本事件具有不可分解的特性,因此也将它称作简单事件(Simple event)。简单事件不必定义,它是随着试验而自然存在的,从而我们可以用所有的简单事件反过来定义理想的试验。
一个复杂事件都可以分解为若干个简单事件的集合,每个事件都可以通过列举它所对应的样本点来描述。于是当子集 $A$ 中某个样本点出现了,就说事件 $A$ 发生了,或者说:
命题 $1$
事件 $A$ 发生当且仅当 $A$ 中某个样本点出现了。
命题 $2$ (样本空间的分割)
在样本空间 ${\mit\Omega}$ 中,若有 $n$ 个事件 $D_1,D_2,\cdots,D_n$,满足:
- $D_1,D_2,\cdots,D_n$ 两两互不相容;
- $\bigcup\limits_{i=1}^{n}D_i={\mit\Omega}$。
则称 $D_1,D_2,\cdots,D_n$ 为样本空间 ${\mit\Omega}$ 的一个分割(Division),称事件 $D_1,D_2,\cdots,D_n$ 为样本空间 ${\mit\Omega}$ 的一个完备互斥事件组。
可列个互不相容的事件 $D_1,D_2,\cdots,D_n,\cdots$ 若满足 $\bigcup\limits_{i=1}^{\infty}D_i={\mit\Omega}$,那么 $D_1,D_2,\cdots,D_n,\cdots$ 也可以成为样本空间 ${\mit\Omega}$ 的一个分割。
联合样本空间
同一个随机现象,由于研究的“侧重点”不同,通常会定义不同的样本空间,这些“侧重点”就是我们研究随机现象所包含的指标(Indicator)、维度(Dimension)或者因子(Factor),不同维度(指标或者因子)本质上描述还是同一个随机现象。
比如要研究“某城市的交通事故”,如果研究的侧重点在于“交通事故的严重程度”,那么样本空间就为
\[{\mit\Omega}_1=\{\text{轻微碰撞},\text{重度碰撞},\text{严重碰撞}\}\]要研究的侧重点在于“一年中发生交通事故的次数”,那么样本空间就为
\[{\mit\Omega}_2=\{0,1,2,\cdots\}\]要研究的侧重点在于“交通事故发生的时间段”,那么样本空间就为
\[{\mit\Omega}_3=\{\text{凌晨},\text{早高峰},\text{中午},\text{晚高峰},\text{夜间}\}\]像这样的“侧重点”可以列出很多个,但是一旦明确了研究的“侧重点”(维度),则样本空间就被确定下来,此时样本空间是唯一且固定的。这意味着不能在同一个维度中使用多个样本空间,否则会导致分析上的混乱。
当然也可以基于不同的研究维度所定义的样本空间,构建联合样本空间(Joint sample space),或者称为重构样本空间(Reconstructed sample space),即将一个较大的、复杂的样本空间细化为更详细的子集来捕捉更具体的信息。比如要同时研究“交通事故的严重程度和时间段”,此时的样本空间则为:
\[{\mathit\Omega}={\mathit\Omega}_1\times{\mathit\Omega}_3=\{(\text{轻微碰撞},\text{凌晨}),(\text{严重碰撞},\text{早高峰}),\cdots\}\]其中 ${\mit\Omega}_1\times{\mit\Omega}_3$ 为两个集合的 Descartes 积,每个样本点都是一个二元组,包含了交通事故的严重程度和时间段。
联合样本空间是对样本空间的不同层次地描述,但这并没有改变样本空间的唯一性,只是对它进行了更细致地表述,以适应不同的分析需要。选择样本空间时,重要的是要确保它包含所有可能的结果。
当我们面对同一个随机现象时,不同样本空间的选择往往意味着对问题的不同维度的不同描述。一旦确定了样本空间,所有事件和概率计算必须基于该样本空间进行,不能在同一维度中混用多个样本空间来描述同一个随机现象。
事件间的关系与运算
下面的讨论总是假设事件 $A$ 与 $B$ 在同一个样本空间 ${\mit\Omega}$ 中进行(即同一个随机现象),我们一般使用 Venn 图来表示事件间的关系与运算。
事件间的关系
事件间的关系与集合间的关系一样,主要有以下几种:
- 包含关系:若属于 $A$ 的样本点必属于 $B$,则称 $A$ 被包含在 $B$ 中,或称 $B$ 包含 $A$,记为 $A\subset B$ 或 $B\supset A$。用概率论的语言说就是:事件 $A$ 发生必然导致事件 $B$ 发生。对于任一事件 $A$,必有 $\boldsymbol{\varnothing\subset A\subset{\mit\Omega}}$;
- 相等关系:若属于 $A$ 的样本点必属于 $B$,并且属于 $B$ 的样本点也必属于 $A$,即 $\boldsymbol{A\subset B}$ 且 $\boldsymbol{B\supset A}$,则称事件 $A$ 与 $B$ 相等,记为 $A=B$。从集合论观点看,两个事件相等就意味着这两事件是同一个集合;
- 互不相容关系:若 $A$ 与 $B$ 没有相同的样本点,则称 $A$ 与 $B$ 互不相容。用概率论的语言说就是:事件$\boldsymbol{A}$ 与事件 $\boldsymbol{B}$ 不可能同时发生。
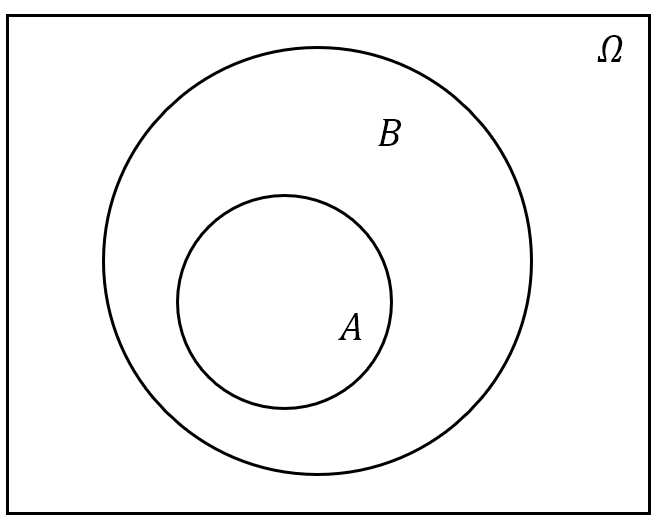
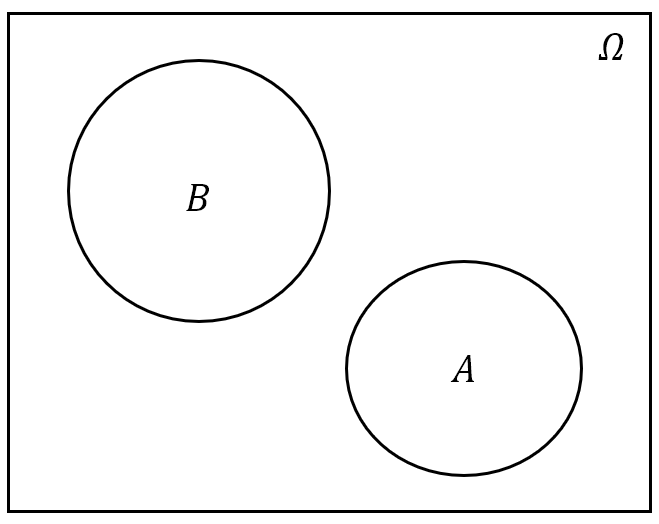
图 2: 事件间的关系
事件的运算
事件的运算与集合的运算相当,有并、交、差和余四种运算。
-
事件 $A$ 与 $B$ 的差:记为 $A-B$,也可以记作 $A\setminus B$ 或者 $A\bar{B}$。其含义为“由在事件 $A$ 中而不在 $B$ 中的样本点组成的新事件”,或用概率论的语言说“事件 $A$ 发生而 $B$ 不发生”;
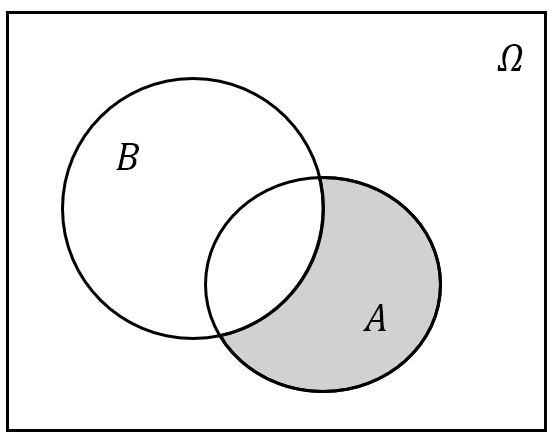
(a) $A-B$ .png)
(b) $A-B(A\supset B)$ 图 3: 事件的差集运算
- 事件 $A$ 与 $B$ 的并:记为 $A\cup B$,也可以记作 $A+B$。其含义为“由事件 $A$ 与 $B$ 中所有的样本点(相同的只计一次)组成的新事件”,或用概率论的语言说“事件 $A$ 与 $B$ 中至少有一个发生”;
- 事件 $A$ 与 $B$ 的交:记为 $A\cap B$,或简记为 $AB$。其含义为“由事件 $A$ 与 $B$ 中公共的样本点组成的新事件”,或用概率论的语言说“事件 $A$ 与 $B$ 同时发生”;
- 对立事件(余集):将事件 $A$ 的对立事件记为 $\bar{A}$,即“由在 $\mit\Omega$ 中而不在 $A$ 中的样本点组成的新事件”,或用概率论的语言说“$A$ 不发生”,即 $\bar{A}={\mit\Omega}-A$。
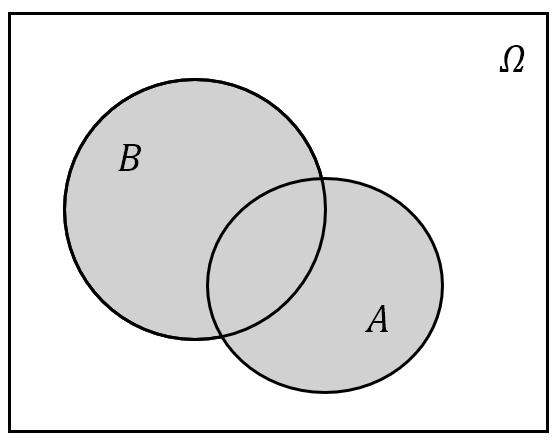
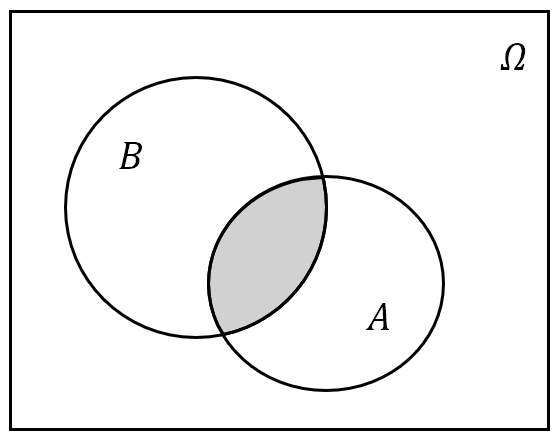
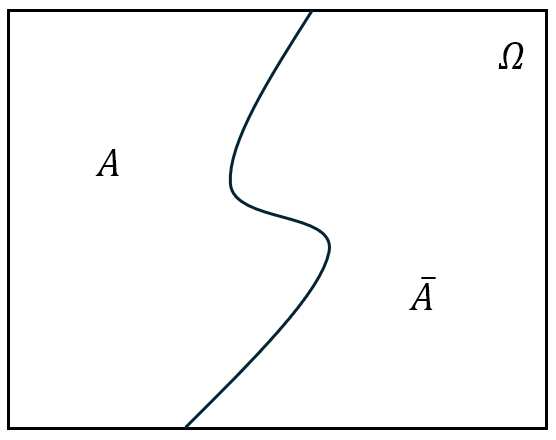
图 4: 事件的交、并与余集运算
需要特别注意的是,对立事件是相互的,也就是说 $A$ 的对立事件是 $\bar{A}$,而 $\bar{A}$ 的对立事件是 $A$,即 $\bar{\bar{A}}=A$。必然事件 ${\mit\Omega}$ 与不可能事件 $\boldsymbol{\varnothing}$ 互为对立事件,即 $\bar{\mit\Omega}=\varnothing$,$\bar{\varnothing}={\mit\Omega}$。
命题 $3$
$A$ 与 $B$ 互为对立事件的充分必要条件是:$A\cap B=\varnothing$,并且 $A\cup B={\mit\Omega}$。
命题 $3$ 也可作为对立事件的另一种定义,即如果事件 $A$ 与 $B$ 满足:$A\cap B=\varnothing$,且 $A\cup B={\mit\Omega}$,则称 $A$ 与 $B$ 互为对立事件,记为 $\bar{A}=B$,$\bar{B}=A$。
对立事件一定是互不相容事件,即 $A\cap\bar{A}=\varnothing$,但是互不相容事件不一定是对立事件。
事件运算的性质
下面设事件 $A,B,C$ 属于同一个样本空间 $\mit\Omega$,那么事件 $A,B,C$ 满足以下性质:
- 交换律: $$ \begin{equation} A \cup B = B \cup A, \quad AB = BA \end{equation} $$
- 结合律: $$ \begin{equation} A\cup(B\cup C)=(A\cup B)\cup C, \quad A(BC)=(AB)C \end{equation} $$
- 分配律: $$ \begin{equation} (A\cup B)\cap C=AC \cup BC, \quad (A\cap B)\cup C=(A\cup C)\cap(B\cup C) \end{equation} $$
- De Morgan 公式: $$ \begin{equation} \overline{A\cup B}=\bar{A} \cap \bar{B},\quad \overline{A\cap B}=\bar{A} \cup \bar{B} \end{equation} $$
De Morgan 公式可推广至 $n$ 个事件以及可列个事件的情况:
\[\begin{equation} \overline{\bigcup_{i=1}^{n}A_i}=\bigcap_{i=1}^{n}\bar{A}_i,\quad \overline{\bigcap_{i=1}^{n}A_i}=\bigcup_{i=1}^{n}\bar{A}_i \end{equation}\] \[\begin{equation} \overline{\bigcup_{i=1}^{\infty}A_i}=\bigcap_{i=1}^{\infty}\bar{A}_i,\quad \overline{\bigcap_{i=1}^{\infty}A_i}=\bigcup_{i=1}^{\infty}\bar{A}_i \end{equation}\]概率的公理化
概率的公理化定义(Probability axioms)是概率论发展的一个重要里程碑,它奠定了现代概率论的基础,彻底改变了过去基于经验和直觉的概率观念。
在 18 世纪初,Jacob Bernoulli 就试图给概率确定一个可计算的公式2。直到 1812 年,Laplace 才将概率定义为3:
\[\begin{equation} P(A)=\frac{\text{有利结果数}}{\text{总结果数}} \end{equation}\]尽管这一定义在简单场景中有效,但它依赖于等可能性的假设,在更多复杂场景下无法推广。这一时期的概率论主要围绕着有限样本空间的等可能事件展开。
时间来到了 19 世纪晚期至 20 世纪,频率学派的概率观逐渐取代古典定义。Richard von Mises 将概率定义为某一事件在大量重复试验中发生的相对频率4,即
\[\begin{equation} P(A)=\lim_{n\to\infty}\frac{n_A}{n} \end{equation}\]其中 $n_A$ 是事件 $A$ 发生的次数,$n$ 是试验的总次数。这一方法突破了古典定义在非等可能情境中的局限性,但也面临一些哲学上的争议,特别是在如何定义“无限次重复”时遇到了困难。
与频率学派同时期,Bayes 提出了基于先验知识更新概率的概念,即 Bayes 定理。Bayes 学派强调概率是对某一随机现象的主观信念程度,主张通过已知证据(即已经发生的事件的信息)来更新这一信念:
\[\begin{equation} P(A\mid B)=\frac{P(A)P(B\mid A)}{P(B)} \end{equation}\]Bayes 学派认为概率不一定源自重复试验,而是基于观察归纳和对先验知识的修正。
1933 年 Kolmogorov 首次提出了基于集合论和测度论的公理化概率定义,标志着概率论进入现代阶段。这个定义概括了历史上几种概率定义中的共同特性,以最少的几条本质特性出发去刻画概率的概念,同时避免了各自的局限性和含混之处。不管什么随机现象,只有满足该定义中的三条公理,才能说它是概率。
Kolmogorov 的公理化体系使用了集合论的语言,将概率视为对一个集合(即样本空间)的子集赋予的测度。他提出的三条公理已经形成了现代概率论的基础。
但在这之前,我们必须首先明确哪些集合可以被称为“事件”,并且构造一个包含在样本空间的“事件集合”。直觉上我们所构造的集合应该对事件的各种运算(即余集、交集和并集)封闭,并且样本空间 ${\mit\Omega}$ 本身和它的余集 $\varnothing$ 都应该在这个“事件集合”中。
事件域
设 ${\mit\Omega}$ 为一个样本空间,$\mathscr{F}$ 是 ${\mit\Omega}$ 的子集所组成的集合类。若 $\mathscr{F}$ 满足:
- ${\mit\Omega}\in\mathscr{F}$;
- 若 $A\in\mathscr{F}$,则对立事件 $\bar{A}\in\mathscr{F}$;
- 若 $A_1,A_2,\cdots,A_n,\cdots\in\mathscr{F}$,则可列并 $\bigcup\limits_{i=1}^{\infty}A_i\in\mathscr{F}$。
则称 $\mathscr{F}$ 是一个事件域(Event field),或者 $\sigma\ -$ 域或者 $\sigma\ -$ 代数。
在概率论中,称 $({\mit\Omega},\mathscr{F})$ 为可测空间(Measurable space),只有在可测空间上才能定义概率,这时 $\mathscr{F}$ 上都是有概率可言的事件。
$\sigma\ -$ 代数用于定义哪些集合可以称为“事件”,并确保可以在这些事件上合理地定义和计算概率。通过 $\sigma\ -$ 代数,我们能对各种复杂事件进行可数次或者有限次运算(余集、交集和并集),并确保这些操作后的结果依然是事件,即仍然在 $\sigma\ -$ 代数中。
需要注意的是,在概率论中,$\sigma\ -$ 代数指的就是那些可以定义概率的事件的集合(并且满足余集和可列并封闭)。至于在其他学科中,有其他学科所赋予的内涵。并且由条件 $(2)$ 可知,$\varnothing\in\mathscr{F}$,并且 $\overline{\bigcup\limits_{i=1}^{\infty}A_i}=\bigcap\limits_{i=1}^{\infty}\bar{A}_i\in\mathscr{F}$。
一维实数轴 $\mathbb{R}$ 上的 Borel 集是常见的 $\sigma\ -$ 代数,它是由一切有界开区间 $(a,b)$,通过至多可数次的(有限或者可数)余集运算、交集运算和并集运算得到的集合。
在实际应用中,$\sigma\ -$ 代数提供了一个框架,它被用于定义一个复杂事件系统,使其可以进行概率分析,这允许我们根据不同的应用场景定义哪些事件是可以赋予概率的。通常一个较大的集合 ${\mit\Omega}$ 可能包含无穷多个子集,而只有 $\sigma\ -$ 代数中的事件才是我们能够赋予概率的“可测事件”。
不仅如此,$\sigma\ -$ 代数还为事件提供了一个良好的数学结构,还确保了我们对事件操作的一致性。由于 $\sigma\ -$ 代数对余集和可数并封闭,所以在定义事件的概率时,无论我们是直接计算事件的概率,还是通过余集或并集的方式来间接计算概率,都能够得到一致的结果。
那些无法精确测量、描述过于复杂或超出我们观察能力的事件,通常不属于 $\sigma\ -$ 代数,因此我们无法为它们赋予概率。这些事件往往涉及无限小区间、无穷复杂现象或超精确测量,在实际概率分析中无法处理,属于不可测事件。例如一个颜色的 RGB 值精确为某个特定数值、在无穷多次抛硬币结果中,硬币的正反面组成某个非常特定的无穷序列。
概率的公理化定义
设 $\mit\Omega$ 为一个样本空间,$\mathscr{F}$ 为 $\mit\Omega$ 上的事件域,$P(A)$ 为定义在 $\mathscr{F}$ 上的实值函数。若$P(A)$ 满足:
- 非负性:$\forall A\in\mathscr{F}$,$P(A)\geqslant0$;
- 正则性:$P({\mit\Omega})=1$;
- 可列可加性:$\forall A_1,A_2,\cdots,A_n,\cdots\in\mathscr{F}$,且 $A_1,A_2,\cdots,A_n,\cdots$ 两两互不相容,则 $$ \begin{equation} P\left(\bigcup_{i=1}^{\infty}A_i\right)=\sum_{i=1}^{\infty}P(A_i) \end{equation} $$
则称 $P(A)$ 为事件 $A$ 的概率(Probability)。
称 $({\mit\Omega},\mathscr{F},P)$ 为概率空间(Probability space),它为研究随机现象提供了一个严谨的数学框架,使我们能够合理地处理、计算和分析各种随机事件的概率。无论是处理简单的随机事件,还是处理复杂的随机变量,都可以在这个框架下进行。
从定义可以看出,概率 $P$ 是事件 $A$ 的实函数,并且概率 $P(A)$ 是有界的,即 $0\leqslant P(A)\leqslant1$。
这一公理化体系与 Lebesgue 测度相结合,使得概率论的基础变得更加坚实,能够处理复杂的事件和连续概率空间问题。Kolmogorov 的公理化定义克服了以往各个学派的局限性,使得概率论从经验和直觉的框架走向了严谨的数学体系。
概率建模的步骤
概率论可以用来分析现实世界的许多不确定现象,这个过程通常分成两个阶段:
- 从一个适当的样本空间中给出概率分布,从而建立概率模型。在这个阶段没有关于建立模型的一般规则,只要建立的概率分布符合概率公理化即可。可能有些人会怀疑所建立模型的真实性,有时人们宁愿使用“错误”的模型,其理由是“错误”的模型比“正确”的模型简单且易于处理,这种处理问题的态度在科学和工程学中很普遍。因此在实际工作中,选择的模型往往既要准确、简单又要兼顾易操作性。此外统计学家还依据历史数据和过去相似试验的结果,利用统计方法确定模型,比如 Bayes 统计;
- 我们将在完全严格的概率模型之下进行推导,计算某些事件的概率或推导出一些十分有趣的性质,$(1)$ 的任务是建立现实世界与数学的联系,而 $(2)$ 则是严格限制在概率公理之下的逻辑推理。如果涉及的计算很复杂或概率分布的陈述不简明,推理和理解就会遇到困难,但是所有的问题将会有一个准确的答案不会产生歧义,只要有足够高的能力,所有的困难都将迎刃而解。
概率的性质
概率的基本性质
下面设事件 $A,B$ 属于同一个样本空间 $\mit\Omega$,由概率的公理化定义容易推出概率的以下性质:
-
不可能事件 $\varnothing$ 的概率为 0:即 $P(\varnothing)=0$;
证明
由于
\[{\mathit\Omega}={\mathit\Omega}\cup\varnothing\cup\cdots\cup\varnothing\cup\cdots\]由概率的可列可加性,
\[P({\mathit\Omega})=P({\mathit\Omega})+P(\varnothing)+\cdots+\varnothing+\cdots\]由于 $P({\mathit\Omega})=1$,因此
\[P(\varnothing)+\cdots+P(\varnothing)+\cdots=0\]又由于概率的非负性,于是 $P(\varnothing)=0$。
概率为 0 的事件并不意味着它是不可能事件,当一个事件的概率为 0 的时候,它也是有一定机会出现的;但是不可能事件的概率为 0,不可能事件是一定不会出现的!
-
有限可加性:若有 $n$ 个两两互不相容的事件 $A_1,A_2,\cdots,A_n$,则 \(\begin{equation} P\left(\bigcup_{i=1}^{n}A_i\right)=\sum_{i=1}^{n}P(A_i) \end{equation}\)
证明
由于
\[A_1\cup A_2\cup\cdots\cup A_n=A_1\cup A_2\cup\cdots\cup A_n\cup\varnothing\cup\cdots\cup\varnothing\cup\cdots\]因此由可列可加性,有
\(\begin{aligned} P\left(\bigcup_{i=1}^{n}A_i\right)&=P(A_1)+P(A_2)+\cdots+P(A_n)+P(\varnothing)+\cdots+P(\varnothing)+\cdots\\ &=P(A_1)+P(A_2)+\cdots+P(A_n) \end{aligned}\)
-
对立事件的概率:对任意事件 $A$,其对立事件 $\bar{A}$ 的概率为 \(\begin{equation} P(\bar{A})=1-P(A) \end{equation}\)
证明
根据对立事件的定义,
\[{\mathit\Omega}=A\cup\bar{A}\quad(\text{或者}\bar{A}={\mathit\Omega}-A)\]因此 $P({\mathit\Omega})=P(A)+P(\bar{A})=1$,即
\[P(\bar{A})=1-P(A)\]结论得证。
事件的差的概率
命题 $4$
对于任意两个事件 $A$ 与 $B$,其差 $A-B$ 的概率为
\[\begin{equation} P(A-B)=P(A)-P(AB) \end{equation}\]证明
由事件的结合律,有
\[A=A\cup(B\cap\bar{B})=AB\cup A\bar{B}=AB\cup(A-B)\]又由于 $AB$ 与 $A-B$ 互不相容,那么
\[P(A)=P(AB)+P(A-B)\]即 $P(A-B)=P(A)-P(AB)$,结论得证。
事件 $A-B$ 也可以写作 $A\bar{B}$,$P(A-B)$ 实际上计算的是 $P(A\bar{B})$ 的值。
推论 $1$
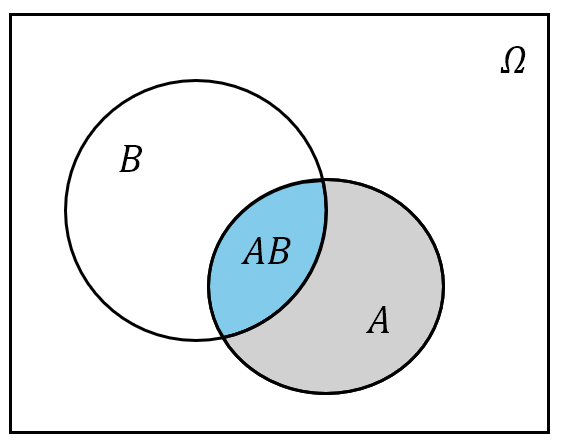
对于任意两个事件 $A$ 与 $B$,若 $B\subset A$,则其差 $A-B$ 的概率为
\[\begin{equation} P(A-B)=P(A)-P(B) \end{equation}\]证明
由于 $B\subset A$,因此 $AB=B$,于是
\[P(A-B)=P(A)-P(B)\]从几何直观上看,求事件 $A-B$ (图中灰色部分)的概率只需用事件 $A$ 的“面积”减去事件 $AB$ 的“面积”:
.png)
图 5: 事件 $A-B$ 的概率的 Venn 图示意
最大号码估计问题
某城有 $n$ 辆卡车,其车牌号从 $1$ 到 $n$。有一个外地人到该城去,把遇到的 $m$ 辆车子的牌号抄下(可能重复抄到某些车牌号)。设事件 $A_i$ 为遇到的 $m$ 辆车子的的最大牌号为 $k$,下面求抄到的最大号码正好为 $k$ 的概率($1\leqslant k\leqslant n$)。
若直接计算 $A_k$ 的概率会比较复杂,因此考虑“遇到的 $m$ 辆车子的最大牌号小于等于 $k$”,将其设为事件 $B_k$,那么 $A_k$ 则可以表示为 $A_k=B_k-B_{k-1}$,并且 $B_{k-1}\subset B_k$。事件 $B_k$ 比起 $A_k$ 的概率要好求得多。根据古典概型可求得事件 $B_k$ 的概率为
\[P(B_k)=\frac{k^m}{n^m}, \quad k=1,2,\cdots,n\]从而
\[P(A_k)=P(B_k-B_{k-1})=P(B_k)-P(B_kB_{k-1})=P(B_k)-P(B_{k-1})=\frac{k^m-(k-1)^m}{n^m}\]推论 $2$ (概率的单调性)
对于任意两个事件 $A$ 与 $B$,若 $B\subset A$,则 $P(B)\leqslant P(A)$。
推论 2 的逆命题不成立,即若 $P(B)\leqslant P(A)$ 无法推出 $B\subset A$。
加法公式
定理 $1$
对于任意的两个事件 $A$ 与 $B$,其交事件 $A\cup B$ (即事件 $A$ 或 $B$ 至少发生一个)的概率为
\[\begin{equation} P(A\cup B)=P(A)+P(B)-P(AB) \end{equation}\]证明
由于
\[A\cup B=A\cup(B-AB)\]又由于 $A\cap (B-AB)=\varnothing$,即 $A$ 与 $B-AB$ 互不相容,则由有限可加性,以及 $AB\subset B$,有
\[P(A\cup B)=P(A)+P(B-AB)=P(A)+P(B)-P(AB)\]从几何直观上看,求事件 $A\cup B$ 的概率就是把事件 $A$ 的“面积”加事件 $B$ 的“面积,但是由于多加了一次事件 $AB$ (图中蓝色部分)的面积,因此必须再额外减去:
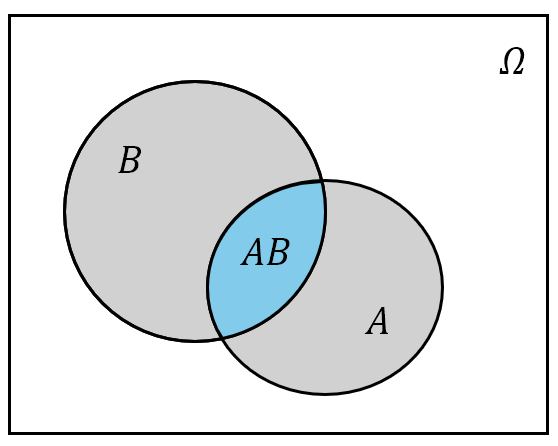
图 6: 事件 $A\cup B$ 的概率的 Venn 图示意
推论 $3$
对于 $n$ 个任意事件 $A_1,A_2,\cdots,A_n$,其交事件的概率为 $\bigcup\limits_{i=1}^{n}A_i$ 的概率为
\[\begin{equation} \begin{aligned} P\left(\bigcup_{i=1}^{n}A_i\right)&=\sum_{i=1}^{n}P(A_i)-\sum_{1\leqslant i\leqslant j\leqslant n}P(A_iA_j)\\ &+\sum_{1\leqslant i\leqslant j\leqslant k\leqslant n}P(A_iA_jA_k)+(-1)^{n-1}P(A_1A_2\cdots A_n) \end{aligned} \end{equation}\]其中一共包含 $\binom{n}{r}$ 个和项。
推论 $4$ (半可加性)
对于任意两个事件 $A$ 与 $B$,有
\[\begin{equation} P(A\cup B)\leqslant P(A)+P(B) \end{equation}\]对于任意 $n$ 个事件 $A_1,A_2,\cdots,A_n$,有
\[\begin{equation} P\left(\bigcup_{i=1}^{n}A_i\right)\leqslant \sum_{i=1}^{n}P(A_i) \end{equation}\]推论 $4$ 也被称为 Boole 不等式。
确定概率的方法
频率的稳定性
确定概率的频率方法是在大量重复试验中,用频率的稳定值去获得概率的一种方法,其基本思想是:
- 与考察事件 $A$ 有关的随机现象可大量重复进行。
- 在 $n$ 次重复试验中,记 $n(A) $为事件 $A$ 出现的次数,又称 $n(A)$ 为事件 $A$ 的频数,称 $$ \begin{equation}\label{eq:极限频率} f_n(A)=\frac{n(A)}{n} \end{equation} $$ 为事件 $A$ 出现的频率(Frequency)。
- 人们的长期实践表明:随着试验重复次数 $n$ 的增加,频率 $f_n(A)$ 会稳定在某一常数 $a$ 附近,我们称这个常数为频率的稳定值,这个频率的稳定值就是我们所求的概率,这个性质被称为频率的稳定性(Stability of frequency)。因此就可以用事件 $A$ 发生的频率来近似事件 $A$ 发生的概率: $$ \begin{equation}\label{eq:频率定义} P(A)=\lim_{n\to\infty}f_n(A)=\lim_{n\to\infty}\frac{n(A)}{n} \end{equation} $$ 由\eqref{eq:频率定义}式定义的概率被称作概率的频率定义(Frequentist probability),拥护此定义的学者或者学派被称为频率学派。
容易验证:由\eqref{eq:极限频率}式定义的“概率”满足非负性与正则性;当事件 $A$ 与 $B$ 不相容时,$n(A\cup B)=n(A)+n(B)$,因此
\[P(A\cup B)=\lim_{n\to\infty}\frac{n(A\cup B)}{n}=\lim_{n\to\infty}\frac{n(A)}{n}+\lim_{n\to\infty}\frac{n(B)}{n}=P(A)+P(B)\]因此\eqref{eq:极限频率}式定义的“概率”的确为可测概率。
随机现象有其偶然性的一面,也有其必然性的一面。这种必然性表现为大量试验中随机事件出现的频率的稳定性,即一个随机事件出现的频率常在某个固定的常数附近摆动,这种规律性我们称之为统计规律性(Statistical regularity)。频率的稳定性说明随机事件发生的可能性大小是随机事件本身固有的、不随人们意志而改变的一种客观属性,因此可以对它进行度量。
例如有人曾对 1930 年至 1988 年世界各地的 53274 场重大足球比赛作了统计:在判罚的 15382 个点球中有 11172 个命中,由此可得罚点球命中率的估计值为
\[P(\text{点球命中})=\frac{\text{点球命中的次数}}{\text{判罚点球的次数}}=\frac{11172}{15382}\approx0.726\]主观概率
在现实世界里有一些随机现象是不能重复的或不能大量重复的,Bayes 学派认为:一个事件的概率是人们根据经验对该事件发生的可能性所给出的个人信念,这样给出的概率称为主观概率(Subjective probability)。
主观给定的概率要符合概率的公理化定义。
例如有一个学者以 90% 的把握断言《伊里亚特》和《奥德赛》是由同一作者创作的,所谓概率为 90% 的把握是学者的主观信念;再比如周五晚上的热门电影,你可能会觉得电影票已经卖完的概率是 60%,这是判断基于你对这个时间段和电影受欢迎程度的理解。
古典概型
古典概型是最早且最直观的一种概率模型,它适用于那些有限个且等可能事件的情境。所谓“古典”,意思是它起源于概率论的早期发展阶段,其基本思想如下:
- 所涉及的随机现象只有有限个样本点;
- 每个样本点发生的可能性相等(称为等可能性);
- 若事件 $A$ 含有 $k$ 个样本点,则事件 $A$ 的概率为 $$ \begin{equation}\label{eq:古典概型} P(A)=\frac{\text{事件}A\ \text{所含样本点的个数}}{\mathit\Omega\ \text{中所有样本点的个数}}=\frac{k}{n} \end{equation} $$ 由\eqref{eq:古典概型}式定义的概率被称作概率的古典定义(Classical probability)。
下面来解释一下基本概型的基本思想的内涵,设 ${\mit\Omega}=\{\omega_1,\omega_2,\cdots,\omega_n\}$,依据基本思想 $(2)$,有
\[\begin{equation} P(\omega_1)=P(\omega_2)=\cdots=P(\omega_n)=\frac{1}{n} \end{equation}\]对于任意事件 $A$,它总可以表示为样本点之交,即 $A=\omega_{i_1}\cup\omega_{i_2}\cup\cdots\cup\omega_{i_m}$,其中 $\omega_{i_1},\omega_{i_2},\cdots,\omega_{i_m}$ 两两互不相容,于是
\[P(A)=P(\omega_{i_1})+P(\omega_{i_2})+\cdots+P(\omega_{i_m})=\frac{m}{n}\]所以在古典概型中,事件 $A$ 的概率的分母是样本点的总数 $n$,而分子是事件 $A$ 中所包含的样本点的个数。由于这 $m$ 个样本点 $\omega_{i_1},\omega_{i_2},\cdots,\omega_{i_m}$ 的出现必导致 $A$ 的出现,即它们的出现对事件 $A$ 的出现“有利”,因此习惯上常称 $\omega_{i_1},\omega_{i_2},\cdots,\omega_{i_m}$ 是 $A$ 的“有利场合”。
容易验证:\eqref{eq:古典概型}式所定义的“概率”满足非负性与正则性,上面也证明了\eqref{eq:古典概型}式的可加性,因此\eqref{eq:古典概型}式所定义的“概率”的确为可测概率。
在古典概型中,求事件 $A$ 的概率归结为计算 $A$ 中含有的样本点的个数和中含有的样本点的总数,所以在计算中经常用到排列组合工具。
不放回抽样模型
一批产品共有 $N$ 件,其中 $M$ 件是不合格品,$N-M$ 件是合格品。从中随机取出 $n$ 件($n\leqslant N$),下面求事件 $A_m=\text{“取出的}n\text{件产品中有}m\text{件不合格品”}$ 的概率($m\leqslant M,n-m\leqslant N-M$)。
我们先计算样本空间 ${\mit\Omega}$ 中样本点的个数,从 $N$ 件中抽取 $n$ 件产品,由于不限抽取次数,因此样本点的个数就为 $\binom{N}{n}$。又由于是随机抽取的,因此每一件产品抽取到的可能性都是相等的。
接下来先计算事件 $A_0,A_1$ 的概率,然后再求出 $A_m$ 的概率。事件 $A_0$ 为取出的 $n$ 件产品中没有不合格品,也就是 $n$ 件产品全部都是从 $N-M$ 件产品中抽取的,于是
\[\begin{equation} P(A_0)=\frac{\binom{N-M}{n}}{\binom{N}{n}} \end{equation}\]事件$A_1$ 为取出的 $n$ 件产品中仅有 1 件不合格品,也就是说要先从 $M$ 件不合格品抽取 1 件不合格品,再从 $N-M$ 件合格品中抽取 $n-1$ 件合格品,那么
- 从 $M$ 件不合格品抽取 1 件不合格品,一共有 $\binom{M}{1}$ 种取法;
- 从 $N-M$ 合格品中抽取 $n-1$ 件合格品,一共有 $\binom{N-M}{n-1}$ 种取法;
根据乘法原理,取出的 $n$ 件产品中仅有 1 件不合格品的取法一共有 $\binom{M}{1}\binom{N-M}{n-1}$ 种,于是
\[\begin{equation} P(A_1)=\frac{\binom{M}{1}\binom{N-M}{n-1}}{\binom{N}{n}} \end{equation}\]于是事件 $A_m$ 为取出的 $n$ 件产品中有 $m$ 件不合格品,要先从 $M$ 件不合格品中抽取 $m$ 件不合格品,一共有 $\binom{M}{m}$ 种取法,再从 $N-M$ 件合格品种抽取 $n-m$ 件合格品,一共用 $\binom{N-M}{n-m}$ 种取法,由乘法原理,事件 $A_m$ 的取法一共有 $\binom{M}{m}\binom{N-M}{n-m}$ 种,于是
\[\begin{equation} P(A_m)=\frac{\binom{M}{m}\binom{N-M}{n-m}}{\frac{N}{n}}, \quad m=1,2,\cdots,r,\quad r=\min\{n,M\} \end{equation}\]盒子模型
设有 $n$ 个球,每个球都等可能地被放到 $N$ 个不同盒子中的任一个,每个盒子所放球数不限。下面我们将分别求
- 在指定的 $n(n\leqslant N)$ 个盒子中各有一球的概率 $p_1$;
- 恰好有 $n(n\leqslant N)$ 个盒子各有一球的概率 $p_2$。
下面我们先来考虑第 1 个问题:
- 只需考虑 $n$ 个球放在 $n$ 个盒子并且每个盒子有且只有一个球的放法,第1个球在 $n$ 个盒子有 $n$ 种放法,第 2 个球在剩下的 $n-1$ 个盒子有 $n-1$ 种放法……到第 $n$ 个球在剩下的第 $n$ 个盒子只有 1 种放法,由乘法原理,$n$ 个球放在 $n$ 个盒子并且每个盒子有且只有一个球的放法共有 $n!$ 种。于是 $$ \begin{equation} p_1=\frac{n!}{N^n} \end{equation} $$
- $(2)$ 与 $(1)$ 的区别在于 $(1)$ 的 $n$ 个盒子是提前指定好的,而 $(2)$ 的 $n$ 个盒子是在试验时随机选取的,并且一共由 $\binom{N}{n}$ 种选取方法。接着再把 $n$ 个球放入这 $n$ 个各自并且每个盒子有且只有一个球,我们在 $(1)$ 已经求出了一共有 $n!$ 放法,于是根据乘法原理,恰好有 $n$ 个盒子各有一球的放法有 $\binom{N}{n}\cdot n!=A_{N}^{n}$,从而 $$ \begin{equation} p_2=\frac{A_{N}^{n}}{N^n}=\frac{N!}{N^n(N-n)!} \end{equation} $$
再考虑第 2 个问题:
下面我们利用盒子模型 $(2)$ 所得的结果考虑下面这个问题:
生日问题
由盒子模型 $(2)$,我们可以计算出 $n$ 个人的生日全不相同的概率 $p_n$ 是多少。易知
\[p_n=\frac{365!}{365^n(365-n)!}=\left(1-\frac{1}{365}\right)\left(1-\frac{2}{365}\right)\cdots\left(1-\frac{n-1}{365}\right)\]- 当 $n$ 很小或者不是很大的时候,右式的交叉项 $\frac{i}{365}\times\frac{j}{365}(i,j=1,2,\cdots,n-1;i\ne j)$ 可以忽略不计,于是 $$ p_n\approx 1-\frac{1+2+\cdots+(n-1)}{365}=1-\frac{n(n-1)}{730} $$
- 当 $n$ 足够大的时候 ($n>27$),由泰勒公式 $\ln{(1-x)}\approx-x$,则 $$ \ln{p_n}\approx-\frac{1+2+\cdots+(n-1)}{365}=-\frac{n(n-1)}{730} $$
例如一个班上 40 人,那么这 40 人的生日都不相同的概率约为 $\exp(-\frac{40\times39}{730})=11.8\%$,也就是说一个班上至少有 2 人生日相同的概率约为 88.2%!进一步计算可知当 $n\geqslant23$ 时,$1-p_n>0.5$,即当人数大于 22 人时,至少有 2 人生日相同的概率已经超过了 50%;当 $n\geqslant60$ 时,几乎可以肯定至少有 2 人生日在同一天!
几何概型
几何概型是古典概型的推广,用于描述在连续空间中随机事件的发生概率。在几何概型中,事件的概率是基于几何特征(如长度、面积或体积)来计算的。几何概型其基本思想是:
- 一个随机现象的样本空间 $\mit\Omega$ 充满某个区域,其度量(长度、面积或体积等)大小可用 $S_{\mit\Omega}$ 表示;
- 任意一点落在度量相同的子区域内(可能位置不同)是等可能性的;
- 若事件 $A$ 为 $\mit\Omega$ 中的某个子区域,且其度量大小可用 $S_A$ 表示,则事件 $A$ 的概率为 $$ \begin{equation}\label{eq:几何概型} P(A)=\frac{S_A}{S_{\mit\Omega}} \end{equation} $$
容易验证,\eqref{eq:几何概型}式所定义的“概率”满足非负性和正则性;当事件 $A$ 与 $B$ 互不相容时,显然有 $S_{A\cup B}=S_A+S_B$,于是
\[P(A\cup B)=\frac{S_{A\cup B}}{S_{\mathit\Omega}}=\frac{S_A}{S_{\mathit\Omega}}+\frac{S_B}{S_{\mathit\Omega}}=P(A)+P(B)\]因此\eqref{eq:几何概型}式所定义的“概率”的确为可测概率。
求几何概率的关键是对样本空间和所求事件 $A$ 用图形描述清楚(一般用平面或空间图形),然后计算出相关图形的度量(一般为面积或体积)。
会面问题
甲乙两人约定在下午6时到7时之间在某处会面,并约定先到者应等候另一个人 20 分钟,过时即离去。记事件 $A$ 为甲乙两人能会面,求两人能会面的概率。
分别用 $x$ 和 $y$ 分别表示甲、乙两人到达约会地点的时间(以 min 为单位),在平面上建立 $xOy$ 直角坐标系。$(x,y)$ 的所有可能取值在边长为 60 的正方形区域内,其面积为 $S_{\mathit\Omega}=60^2$,而事件 $A=\text{“两人能够会面”}$ 等价于
\[|x-y|\leqslant20\]其面积为 $S_A=60^2-40^2$。根据几何概型有
\[P(A)=\frac{S_A}{S_{\mathit\Omega}}=\frac{60^2-40^2}{60^2}\approx 0.5556\]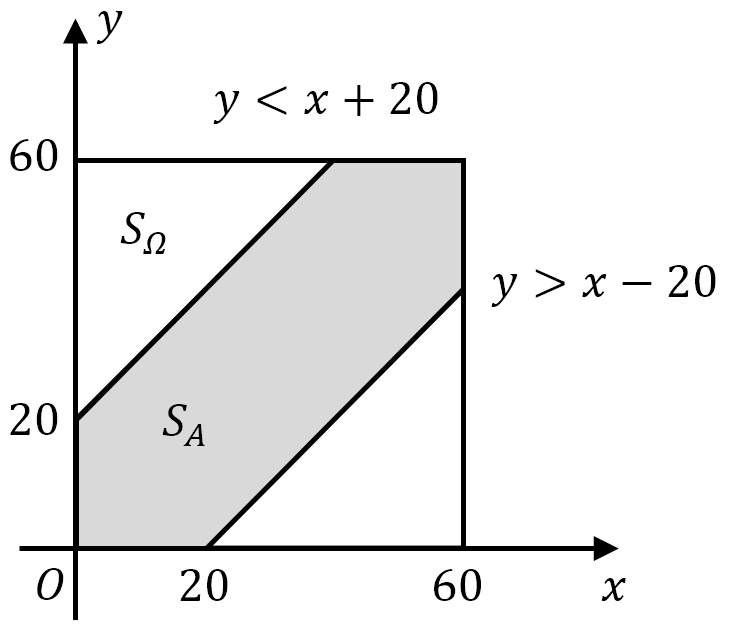
图 7: 会见问题的样本空间
Buffon 投针问题(估计圆周率 $\pi$)
平面上画有间隔为 $d(d>0)$ 的等距平行线,向平面任意投掷一枚长为 $l(l< d)$ 的针。记事件 $A$ 为针与任一平行线相交,下面我们求针与任一平行线相交的概率。
设 $x$ 为针的中点到最近平行线的垂直距离,$\varphi$ 为针与最近平行线所形成的夹角,于是样本空间 $\mit\Omega$ 就为
\[{\mathit\Omega}=\left\{(x,\varphi)\mid 0\leqslant x\leqslant\frac{d}{2},0\leqslant\varphi\leqslant\pi\right\}\]易知针与平行线相交的充分必要条件是:
\[\begin{equation} x\leqslant\frac{l}{2}\sin{\varphi} \end{equation}\]于是由几何概型可知
\[P(A)=\frac{S_A}{S_{\mathit\Omega}}=\frac{\displaystyle\int_{0}^{\pi}\frac{l}{2}\sin{\varphi}}{\frac{d}{2}\pi}=\frac{2l}{d\pi} \ (l<d)\]其中 $l,d$ 为已知量,只需将 $\pi$ 代入即可计算出 $P(A)$ 的值;反过来若已经用事件 $A$ 发生的频率 $\frac{n}{N}$ 估计出了 $P(A)$ 的值,则可以反解出 $\pi$ 来,即
\[\begin{equation} \pi\approx\frac{2lN}{dn} \ (l<d) \end{equation}\]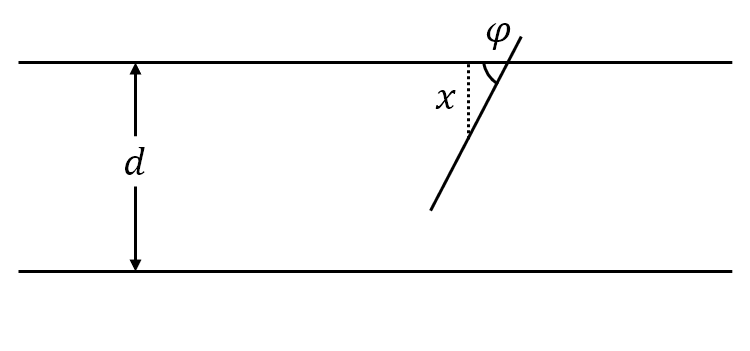
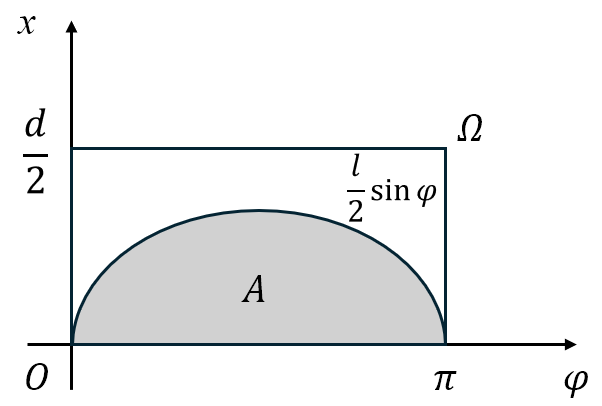
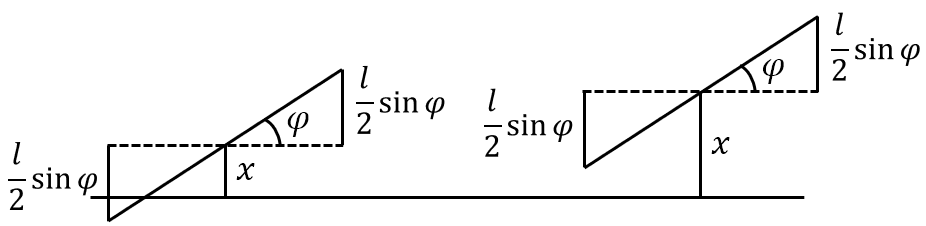
图 8: Buffon 投针
这是一个颇为奇妙的方法:只要设计一个随机试验,使一个事件的概率与某个未知数有关,然后通过重复试验,以频率估计概率,即可求得未知数的近似解。
一般来说试验次数越多,则求得的近似解就越精确,随着计算机的出现,人们便可利用计算机来大量重复地模拟所设计的随机试验。这种方法得到了迅速的发展和广泛的应用,人们称这种方法为随机模拟法,也称为 Monte Carlo 法。Buffon 投针的随机模拟详见 Buffon 投针的计算机模拟。
Bertrand 悖论
在圆内任取一条弦,问其长度超过该圆内接等边三角形的边长的概率是多少?该问题可以有三种不同的解法:
- 假定弦的中点在直径上均匀分布,直径上的点组成样本空间 ${\mit\Omega}_1$。由于对称性可只考察某指定方向的弦,作一条直径垂直于这个方向。显然只有交直径于 $\frac{1}{4}$ 与 $\frac{3}{4}$ 之间的弦才能超过正三角形的边长,因此概率为 $\frac{1}{2}$。
- 假定弦的另一活动端点在圆周上均匀分布,圆周上的点组成样本空间 ${\mit\Omega}_2$。由于对称性可让弦的一端点固定,让另一端点在圆周上作随机移动。若在固定端点作一切线,则与此切线夹角在 $60^{\circ}$ 与 $120^{\circ}$之间的弦才能超过正三角形的边长,因此概率为 $\frac{1}{3}$。
- 假定弦的中点在大圆内均匀分布,大圆内的点组成样本空间 ${\mit\Omega}_3$。圆内弦的位置被其中点唯一确定。在圆内作一同心圆,其半径仅为大圆半径的一半,则大圆内弦的中点落在小圆内,此弦长才能超过正三角形的边长,因此概率为 $\frac{1}{4}$。
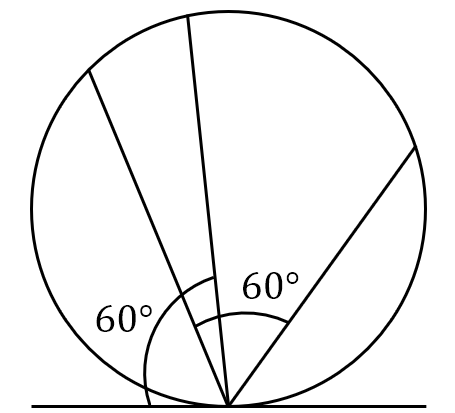
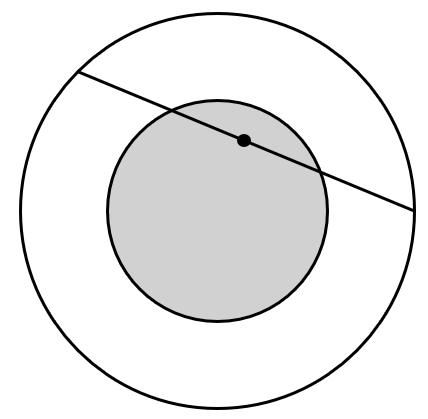
图 9: Bertrand 悖论的三种解法
上述三个答案是针对三个不同样本空间引起的,它们都是正确的,Bertrand 悖论启发我们,在定义概率时要事先明确指出样本空间是什么!
条件概率
条件概率的定义
条件概率(Conditional probability)是在给定部分信息的基础上对试验结果一种推断,当然也可以由试验结果反推试验原因的一些性质与可能性,这就是 Bayes 统计的研究内容了。
用更确切的话说,给定一个试验与这个试验相对应的样本空间和概率分布,假设我们已经知道给定的事件 $B$ 发生了,希望知道另一个给定的事件 $A$ 发生的可能性。因此我们要构造一个新的概率分布,它顾及了事件 $B$ 已经发生的信息,求出任何事件 $A$ 发生的概率。
例如在 $N$ 个人的总体中,有 $N_A$ 个色盲,另外有 $N_H$ 个女性。设事件 $A$ 为“在总体中随机抽取一人为色盲”,事件 $H$ 为“在总体中随机抽取一人为女性”,那么则有
\[P(A)=\frac{N_A}{N},\quad P(H)=\frac{N_H}{N}\]现在用“所有女性”组成的子集(称为子总体)来代替总体,求在这个子总体中随机抽取一人为色盲的概率,显然这个概率为 $\frac{N_{AH}}{N_H}$,其中 $N_{AH}$ 为女性色盲的人数。这里我们并没有提出什么新的概念,只是针对特定的研究内容,所圈定的样本范围有所不同罢了。我们用一个新的记号来表述这个概率:
\[P(A\mid H)\coloneqq\frac{N_{AH}}{N_H}=\frac{P(AH)}{P(H)}\]解释为“在抽取性别为女性的假设条件下,这个人是色盲的概率”。
条件概率
设 $A$ 与 $B$ 是样本空间 $\mit\Omega$ 中的任意两个事件,若 $P(B)>0$,则称
\[\begin{equation} P(A\mid B)=\frac{P(AB)}{P(B)} \end{equation}\]为“在 $B$ 发生的条件下 $A$ 发生”的概率,简称为条件概率。
为了与条件概率相对应,$P(A)$ 可以被称作无条件概率(Unconditional probability)。条件概率 $P(A\mid B)$ 可理解为由于事件 $B$ 的发生,样本空间从 $\boldsymbol{\mit\Omega}$ 变为了 $\boldsymbol{\mit\Omega_{B}=B}$。从几何直观上看,无条件概率 $P(A)$ 就是事件 $A$ (图中灰色部分)占样本空间 ${\mit\Omega}$ 的比例,条件概率 $P(A\mid B)$ 就是事件 $AB$ 的“面积”占事件 $B$ (图中橙色部分加上事件 $AB$ 的灰色部分)的“面积”的比例:
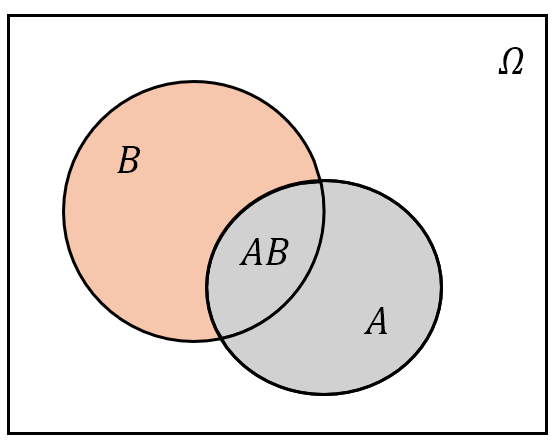
图 10: 条件概率 $P(A\mid B)$ 的 Venn 图示意
显然,每一个子总体本身总可以被考虑为一个总体。为了语言上的方便,在说一个子总体时,意思就是说背后还有一个较大的总体。
在通常意义下,若 $P(B)=0$,那么条件概率 $P(A\mid B)$ 则无法定义或者无意义,也就是说若事件 $B$ 根本不可能发生,那么以事件 $B$ 作为前提来讨论事件 $A$ 的发生情况就不再有意义。不过在测度论的框架下,对于零概率事件的条件概率有更为复杂的处理方法,如 Radon-Nikodym 导数,但这是在更抽象的数学背景下讨论的。
肝癌的医学检测问题
在肝癌普查中发现,某地区的自然人群中,每十万人内平均有 40 人患原发性肝癌,有 34 人甲胎球蛋白高含量,32人既患原发性肝癌又出现甲胎球蛋白高含量。设事件 $A$ 为患肝癌,事件 $B$ 为甲胎球蛋白高含量,那么 $P(A)=0.0004,P(B)=0.00034,P(AB)=0.00032$,从而
\[P(A\mid B)=\frac{P(AB)}{P(B)}=\frac{0.00032}{0.00034}=0.9412, \quad P(B\mid A)=\frac{P(AB)}{P(A)}=\frac{0.00032}{0.0004}=0.8\]$P(B\mid A)=0.8$ 这说明患肝癌的人群中有 80% 的人会有甲胎球蛋白高含量的症状,因此检测甲胎球蛋白的含量能够很好地判断一个人是否患肝癌;而 $P(A\mid B)=0.9412$ 说明若出现了甲胎球蛋白高含量的症状,那么对一个人患肝癌的概率判断的正确性高达 94.12%。
由于事件 $B$ 的发生,使事件 $A$ 发生的概率由 0.0004 一下子上升到 0.9412。可见事件发生的概率,与条件有关,也与已知信息有关。
命题 $5$
设 $P(B)>0$,若
- $\forall A\in\mathscr{F}$,有 $P(A\mid B)\geqslant0$;
- $P({\mit\Omega}\mid B)=1$;
- 若 $\forall A_1,A_2,\cdots,A_n\in\mathscr{F}$,且 $A_i$ 与 $A_j$ 之间两两之间互不相容($i,j=1,2,\cdots,n;i\neq j$); $$ \begin{equation} P\left(\bigcup_{i=1}^{n}A_i\mid B\right)=\sum_{i=1}^{n}P(A_i\mid B) \end{equation} $$
则条件概率 $P(A\mid B)$ 是定义在概率空间 $({\mit\Omega},\mathscr{F},P)$ 上的概率。
因此类似于无条件概率,条件概率也可由三个基本性质导出其他些性质,例如:
- $P(\varnothing\mid B)=0$;
- $P(A\mid B)=1-P(\bar{A}\mid B)$;
- 对于任意两个事件 $A_1$ 与 $A_2$,有 $P(A_1\cup A_2\mid B)=P(A_1\mid B)+P(A_2\mid B)-P(A_1A_2\mid B)$。
乘法公式
乘法公式(Multiplication formula)是计算两个事件同时发生的概率的工具,它将两个事件的联合概率分解为两个步骤:首先计算事件 $B$ 发生的概率,然后计算在 $B$ 发生的前提下事件 $A$ 发生的概率。这种分解能从局部的角度理解复杂的联合概率,其意义在于它可以分步骤计算复杂的联合概率,揭示了事件之间的相互依赖关系。
乘法公式
设 $A$ 与 $B$ 是两个任意事件,若 $P(B)>0$,那么
\[\begin{equation} P(AB)=P(B)P(A\mid B) \end{equation}\]由条件概率的定义式可知,
\[\begin{equation} P(AB)=P(B)P(A\mid B)=P(A)P(B\mid A) \end{equation}\]那么则有
\[\begin{equation} P(A\mid B)=\frac{P(A)}{P(B)}\cdot P(B\mid A) \end{equation}\]也就是说 $P(A\mid B)$ 与 $P(B\mid A)$ 的关系是依靠调整因子 $\frac{P(A)}{P(B)}$ 联系在一起的,并且 $P(A\mid B)$ 与 $P(B\mid A)$ 的比例就是 $\frac{P(A)}{P(B)}$ 的值,这能够让我们清楚地了解是事件 $A$ 影响事件 $B$ 的因素大,还是事件 $B$ 影响事件 $A$ 的因素大。
若事件 $A$ 与事件 $B$ 之间不是独立发生的两个事件,乘法公式也体现了一个事件的发生如何影响另一个事件的发生概率。通过计算条件概率 $P(A\mid B)$ 可以准确估计联合概率。若事件 $A$ 与事件 $B$ 是独立的,即 $P(A\mid B)=P(A)$,则有 $P(AB)=P(A)\cdot P(B)$,这正是独立事件的定义。
推论 $5$
若 $P(A_1A_2\cdots A_{n-1})>0$,那么
\[\begin{equation} P(A_1A_2\cdots A_n)=P(A_1)P(A_2\mid A_1)P(A_3\mid A_1A_2)\cdots P(A_n\mid A_1A_2\cdots A_{n-1}) \end{equation}\]证明
由于
\[\begin{aligned} P(A_1A_2\cdots A_n)&=P(A_1A_2\cdots A_{n-1})P(A_n\mid A_1A_2\cdots A_{n-1})\\ &=P(A_1A_2\cdots A_{n-2})P(A_{n-1}\mid A_1A_2\cdots A_{n-2})P(A_n\mid A_1A_2\cdots A_{n-1})\\ &=\cdots\cdots\\ &=P(A_1)\cdots P(A_{n-1}\mid A_1A_2\cdots A_{n-2})P(A_n\mid A_1A_2\cdots A_{n-1}) \end{aligned}\]又由于
\[P(A_1)\geqslant P(A_1A_2)\geqslant \cdots\geqslant P(A_1A_2\cdots A_{n-1})>0\]因此 $P(A_2\mid A_1),P(A_3\mid A_1A_2),\cdots,P(A_n\mid A_1A_2\cdots A_{n-1})$ 都是有意义的。
三门问题
你站在三个封闭的门前,其中一个门后有奖品,当然奖品在哪一个门后是完全随机的。当你选定一个门以后,主持人打开其余两扇门中的一扇空门,显示门后没有奖品。此时你可以有两种选择,保持原来的选择或者改选另一扇没有被打开的门。
当你作出最后选择以后,如果打开的门后有奖品,这个奖品就归你。现在有三种策略:
- 坚持原来的选择;
- 改选另一扇没有被打开的门;
- 你首先选择 1 号门,若主持人打开的是 2 号门,你则坚持原来的选择,若主持人打开的是 3 号门,你则选择 2 号门。
设事件 $A_i$ 为“第 $i$ 次选择的门后有奖品”,下面分别计算各种策略之下赢得奖品的概率:
- 此策略赢得奖品的概率完全取决于你初始选择的门,因此赢得奖品的概率为 $P(A_1)=\frac{1}{3}$;
- 第一步必须选择一扇门后没有奖品的门,其概率为 $P(\bar{A}_1)=\frac{2}{3}$,第二步你改选另一扇没有没打开的门,其门后有奖品的概率为 $P(A_2\mid \bar{A}_1)=1$,于是由乘法公式,赢得奖品的概率为 $P(\bar{A}_1A_2)=\frac{2}{3}$;
- 在此策略中由于提供的信息不够充分(赢得奖品的概率依赖于主持人打开门的方式),因此再分为以下两种情况讨论:
- 假设主持人始终会打开 2 号门(当奖品在 2 号门时,主持人则会打开其他号门)。假定奖品在 1 号门后(其概率为 $\frac{1}{3}$),主持人则会打开 2 号门,这时赢得奖品的概率为 $P(A_1)=\frac{1}{3}$;假定奖品在 2 后门后,主持人打开 3 号门,这时赢得奖品的概率为 $P(\bar{A}_1A_2)=\frac{1}{3}$;假定奖品在 3 号门后,主持人打开 2 号门,这时赢得奖品的概率为 $0$。于是由加法原理,赢得奖品的概率为 $\frac{1}{3}+\frac{1}{3}=\frac{2}{3}$。
- 假设主持人会随机地打开 2 号门或者 3 号门。假定奖品在 1 号门后(其概率为 $\frac{1}{3}$),主持人随机打开 2 号门或者 3 号门(其概率为 $\frac{1}{2}$),这时赢得奖品的概率为 $P(A_1)=\frac{1}{6}$;假定奖品在 2 号门后,主持人随机打开 2 号门或者 3 号门,这时赢得奖品的概率为 $P(\bar{A}_1A_2)=\frac{1}{3}$;假定奖品在3号门后,主持人随机打开 2 号门或者 3 号门,这时赢得奖品的概率为 $0$。于是由加法原理,赢得奖品的概率为 $\frac{1}{6}+\frac{1}{3}=\frac{1}{2}$。
综上所述,当主持人打开了一扇空门之后,最好的策略是改选另一扇没有被打开的门,此时赢得奖品的概率为 $\frac{2}{3}$。
三门问题的随机模拟详见三门问题的计算机模拟。
全概率公式
全概率公式(Law of total probability)将事件的概率分解为多个条件下的概率,从而提供了一种结构化的计算方式,可以更有效地计算复杂情境下的概率。它特别适合处理多个互不相容的子事件,在这些不同的子事件中包含另一个事件总的发生概率。
全概率公式
设 $A$ 是一个任意事件,若 $B_1,B_2,\cdots,B_n$ 是样本空间 $\mit\Omega$ 的一个分割,即 $B_1,B_2,\cdots,B_n$ 两两之间互不相容,且 $\bigcup\limits_{i=1}^{n}B_i={\mit\Omega}$。若 $P(B_i)>0(i=1,2,\cdots,n)$,则 $A$ 发生的概率为
\[\begin{equation} P(A)=\sum_{i=1}^{n}P(B_i)P(A\mid B_{i}) \end{equation}\]证明
由于 $B_1,B_2,\cdots,B_n$ 构成样本空间 ${\mit\Omega}$ 的一个分割,于是
\[A=A{\mathit\Omega}=A\left(\bigcup_{i=1}^{n}B_i\right)=\bigcup_{i=1}^{n}(AB_i)\]又由于 $B_1,B_2,\cdots,B_n$ 两两之间不互相容,因此 $(AB_1)\cap(AB_2)\cap\cdots\cap(AB_n)=\varnothing$,从而 $AB_1,AB_2,\cdots,AB_2$ 两两之间也互不相容,于是
\[P(A)=\sum_{i=1}^{n}P(AB_i)\]由乘法公式
\[P(AB_i)=P(B_i)P(A\mid B_i)\quad i=1,2,\cdots,n\]因此
\[P(A)=\sum_{i=1}^{n}P(B_i)P(A\mid B_i)\]可以把全概率公式理解为“加权平均”的过程:事件 $A$ 的总概率是基于不同情况 $B_1,B_2,\cdots,B_n$ 下发生的可能性,以及在这些情景下事件 $A$ 发生的条件概率,通过每种情况 $B_i(i=1,2,\cdots,n)$ 下发生的概率 $P(B_i)$ 来对相对应的条件概率 $P(A\mid B)$ “加权”,最终得到事件 $A$ 的总概率。
要求 $\sum\limits_{i=1}^{n}P(B_i)=1$,解释为对应的条件概率的权重,体现各条件概率的重要程度或者贡献度。
$B_1,B_2,\cdots,B_n$ 不必为 $\mit\Omega$ 的一个分割,只需 $B_1,B_2,\cdots,B_n$ 是两两互不相容的事件,且 $A\subset\bigcup\limits_{i=1}^{n}B_i$ 即可;另外可列个 $B_1,B_2,\cdots,B_n,\cdots$ 是两两互不相容的事件,且 $A\subset\bigcup\limits_{i=1}^{\infty}B_i$,则全概率公式依旧成立;
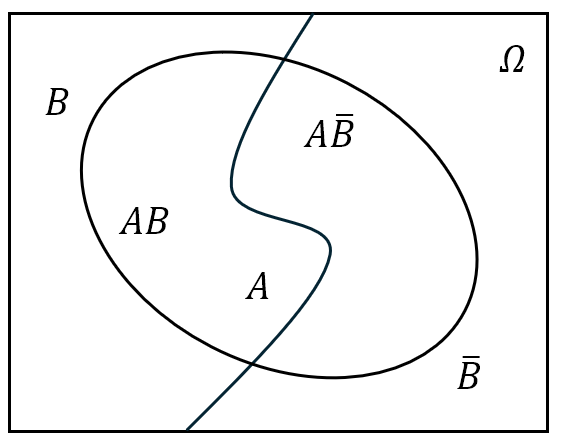
图 11: 不同形式的全概率公式
社会调查中的敏感性调查问题
在社会调查中,若调查内容包含有隐私性问题,被调查者通常不愿意直接回答。例如在校园中调查学生接触过黄色书刊或者影像是否会影响其身心健康发展的课题,从调查数据中估计出学生中解出过黄色书刊或者影像的比例 $p$,为此需要制作两份不同的调查问卷:
- 你的生日是否在 7 月 1 日之前?
- 你是否接触过黄色书刊或者影像?
调查员只需向被调查者随机地出示这两份问卷的其中之一(比如将问卷放入小球中,让被调查者随机地抽取小球);被调查者只需回答“是”或者“否”,然后让其在答卷上勾选自己所认同的答案即可。这样旁人就无法得知被调查者回答的是问题 $(1)$ 还是问题 $(2)$,从而极大地打消了被调查者的心理顾虑,使得调查结果更为准确。
下面假设一共收到了 $n$ 张答卷,其中有 $k$ 张回答“是”,但是我们无法得知 $n$ 张答卷中有多少回答了问题 $(2)$,也不知道 $k$ 中回答“是”的答卷中有多少回答了问题 $(2)$。但是我们可以提前设定的是:
- 在 $n$ 充分大时,任意一人的生日在 7 月 1 日之前的概率应该为 $0.5$;
- 控制问题 $(2)$ 占总体的比率 $\pi$;
于是我们可以利用全概率公式解出 $p$:
\[\begin{aligned} P(\text{是})&=P(\text{问题(1)})P(\text{是}\mid\text{问题(1)})+P(\text{问题(2)})P(\text{是}\mid\text{问题(2)})\\ &=0.5(1-\pi)+\pi p \end{aligned}\]其中 $P(\text{是})$ 可以用频率 $\frac{k}{n}$ 代替(当 $n$ 充分大时),因此
\[\frac{k}{n}=0.5(1-\pi)+\pi p\]从而
\[p=\frac{k/n-0.5(1-\pi)}{\pi}\]例如在一次调查中,设置问题 $(2)$ 的比率为 $\pi=0.6$;共回收 1583 份问卷,其中有 389 份答卷回答了“是”,那么就可以估计出 $p$ 的值:
\[p=\frac{389/1583-0.2}{0.6}=0.0762\]即大约有 7.62% 的学生接触过黄色书刊或者影像。
双胞胎同性别的估计
双胞胎可能是同卵双生或者异卵双生,为了知道双胞胎中同卵双生所占的比例,统计学家首先要求市里每一家医院对双胞胎做记录,同时对是否是同卵双生做标记,然而判断一个新生儿是否是同卵双生并不是一件简单的事,这关系到父母是否愿意自费给孩子做这项复杂而又昂贵的 DNA 检验。而后统计学家只让医院提供标记着双胞胎是否是相同性别的所有双胞胎数据列表。经过计算,当约有 64% 的双胞胎是性别相同时,统计学家就宣称约有 28% 的双胞胎是同卵双生。
下面我们来解释一下其中的原理:首先统计学家假设同卵双生双胞胎性别总是相同的(事实上同卵双生双胞胎几乎总是相同性别的)。又因为异卵双生双胞胎就相当于普通的兄弟姐妹,所以性别相同的概率也有 $\frac{1}{2}$。令事件 $I$ 表示“同卵双生双胞胎”,令事件 $SS$ 表示“双胞胎性别相同”,他在双胞胎是否为同卵双生的条件下计算概率 $P(SS)$,得到
\[\begin{aligned} P(SS)&=P(I)P(SS\mid I)+P(\bar{I})P(SS\mid \bar{I})\\ &=1\times P(I)+\frac{1}{2}\times[1-P(I)]\\ &=\frac{1}{2}+\frac{1}{2}P(I) \end{aligned}\]于是当 $P(SS)\approx0.64$ 时,$P(I)\approx0.28$,即当约有 64% 的双胞胎是性别相同时,则约有 28% 的双胞胎是同卵双生。
Bayes 公式
首先我们先来探究 $P(A)$ 与 $P(\bar{A})$、$P(A\mid B)$ 与 $P(\bar{A}\mid B)$ 的关系:
优势比
设事件 $A$ 发生的概率为 $P(A)$,那么事件 $A$ 的优势比(Odds ratio)则为
\[\begin{equation} \frac{P(A)}{P(\bar{A})}=\frac{P(A)}{1-P(A)} \end{equation}\]事件 $A$ 的优势比告诉我们事件 $A$ 发生的可能性是不发生时的可能性的倍数,若 $P(A)=\frac{2}{3}$,那么 $P(A)=2P(\bar{A})$。如果某事件的优势比等于 $\alpha$,那么通常称支持假设(事件)成立的优势比为“$\alpha:1$”。
考虑假设(事件) $H$ 以概率 $P(H)$ 成立,如果我们发现了新的证据 $E$ (假设 $H$ 发生所依赖的辅助事件),那么在 $E$ 发生的条件下,$H$ 成立和 $H$ 不成立的条件概率分别为
\[P(H\mid E)=\frac{P(H)P(E\mid H)}{P(E)}, \quad P(\bar{H}\mid E)=\frac{P(\bar{H})P(E\mid \bar{H})}{P(E)}\]因此引进证据 $E$ 后,假设 $H$ 的新的优势比为
\[\begin{equation} \frac{P(H\mid E)}{P(\bar{H}\mid E)}=\frac{P(H)}{P(\bar{H})}\cdot\frac{P(E\mid H)}{P(E\mid\bar{H})} \end{equation}\]即 $H$ 的新的优势比值等于它原来的优势比的值乘以新的证据在 $H$ 和 $\bar{H}$ 之下的条件概率比值。如果
\[P(E\mid H)>P(E\mid\bar{H})\]则 $H$ 的优势比值是递增的,反之 $H$ 的优势比是递减的。
新证据对假设的影响
一个坛子里装了两枚 $A$ 型硬币和一枚 $B$ 型硬币,当抛 $A$ 型币时,正面向上的概率是 $\frac{1}{4}$。当抛 $B$ 型硬币时,正面向上的概率是 $\frac{3}{4}$。随机从坛子里取一枚硬币掷,假定掷出的结果是正面向上,下面求所掷的是 $A$ 型硬币的概率是多少。
令事件 $A$ 为“投掷的硬币为 $A$ 型硬币”,事件 $B$ 为“投掷的硬币为 $B$ 型硬币”,并且易知 $\bar{A}=B$,用 head 表示“投掷结果为正面向上”,那么事件 $A$ 的优势比为
\[\frac{P(A\mid \text{head})}{P(\bar{A}\mid \text{head})}=\frac{P(A)}{P(\bar{A})}\cdot\frac{P(\text{head}\mid A)}{P(\text{head}\mid \bar{A})}=\frac{2}{3}\]即在硬币正面朝上的情况下事件 $A$ 的优势比为 $\frac{2}{3}:1$,或者说在硬币正面朝上的情况下事件 $A$ 发生的概率为 $\frac{2}{5}$。
在没有任何信息的情况下,我们判断事件 $A$ 发生的概率为 $\frac{2}{3}$;而在已经知道硬币正面朝上的信息下,我们能用“硬币正面朝上”这个事件的信息量更新判断事件 $A$ 发生的概率为 $\frac{2}{5}<\frac{2}{3}$,这说明“硬币正面朝上”这一个信息对我们判断硬币种类没有任何帮助,反而还会被“硬币正面朝上”这个冗余的信息扰乱我们的视线。
下面考虑新的证据如何影响某个特定假设成立的概率的问题,令事件 $H$ 表示“某个特定假设”,而事件 $E$ 表示“新的证据”,那么
\[\begin{equation}\label{eq:两个对立事件的Bayes公式} P(H\mid E)=\frac{P(E\mid H)P(H)}{P(H)P(E\mid H)+P(E\mid \bar{H}) [1-P(H)]} \end{equation}\]其中 $P(H)$ 为在新证据展示之前我们对假设成立的可能性的估值。新证据支持假设成立,如果它使得假设成立的可能性增大,即 $P(H\mid E)\geqslant P(H)$。于是
\[\begin{equation} P(E\mid H)\geqslant P(H)P(E\mid H)+P(E\mid \bar{H}) [1-P(H)] \end{equation}\]进一步
\[\begin{equation} P(E\mid H)\geqslant P(E\mid \bar{H}) \end{equation}\]即当假设成立时,新证据发生的概率大于假设不成立时发生的概率,就认为新证据支持假设。事实上,已知新的证据发生的条件下,假设成立的新概率和初始概率的关系可从下式看出:
\[\begin{equation} P(H\mid E)=\frac{P(H)}{P(H)+[1-P(H)]\frac{P(E\mid \bar{H})}{P(E\mid H)}} \end{equation}\]\eqref{eq:两个对立事件的Bayes公式}式的分母实际上为 $P(E)=P(H)P(E\mid H)+P(\bar{H})P(E\mid\bar{H})$,只包含了事件 $H$ 与其对立事件 $\bar{H}$;分子实际上为 $P(HE)=P(H)P(E\mid H)$。可以将其推而广之,于是就有下面的 Bayes 公式(Bayesian probability):
Bayes 公式
设 $B_1,B_2,\cdots,B_n$ 是样本空间 $\mit\Omega$ 的一个分割,即 $B_1,B_2,\cdots,B_n$ 是两两之间互不相容的事件,且 $\bigcup\limits_{i=1}^{n}B_i={\mit\Omega}$。若 $P(A)>0$,且 $P(B_i)>0(i=1,2,\cdots,n)$,那么
\[\begin{equation} P(B_i\mid A)=\frac{P(B_i)P(A\mid B_i)}{\sum\limits_{j=1}^{n}P(B_j)P(A\mid B_j)} \end{equation}\]证明
由条件概率的定义
\[P(B_i\mid A)=\frac{P(AB_i)}{P(A)}, \quad i=1,2,\cdots,n\]分子与分母分别用乘法公式和全概率公式代入,即得
\[P(B_i\mid A)=\frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A\mid B_i)}{\sum\limits_{j=1}^{n}P(B_j)P(A\mid B_j)}, \quad i=1,2,\cdots,n\]假定 $B_1,B_2,\cdots,B_n$ 是导致试验结果的各种“原因”,$P(B_i)$ 称之为先验概率(Prior probability),是事件 $B_i$ 没有任何经验或者知识的情况下的概率,它反映了各种“原因”发生的可能性,一般是对以向经验的总结。
在试验中发生了事件 $A$,这个信息将有助于探讨事件发生的“原因”,于是将 $P(B_i\mid A)$ 称之为 $B_i$ 的后验概率(Posterior probability),是通过事件 $A$ 发生的条件下,用事件 $A$ 的经验或者知识来修正先验概率 $P(B_i)$,它反映了试验之后对各种“原因”发生的可能性大小的新知识。
$P(A\mid B_i)$ 称之为事件 $A$ 发生的似然概率5(Likelihood),似然概率可以看作是对因果关系的一种量化。而 $P(A)$ 则被称为事件 $A$ 发生的边际概率(Marginal likelihood)。
肝癌医学检验的可靠性问题
某地区居民的肝癌发病率为 0.0004,现用甲胎蛋白法进行普查。医学研究表明,化验结果是可能存有错误的。已知患有肝癌的人其化验结果 99% 呈阳性,而没患肝癌的人其化验结果 99.9% 呈阴性。现某人的检查结果呈阳性,问他真的患肝癌的概率是多少?
设事件 $A$ 为患肝癌,事件 $B$ 为化验结果为阳性。则
\[P(A)=0.0004, \quad P(B\mid A)=0.99, \quad P(\bar{B}\mid \bar{A})=0.999\]于是 $P(B\mid \bar{A})=0.001$,因此
\[P(A\mid B)=\frac{P(AB)}{P(B)}=\frac{P(A)P(B\mid A)}{P(A)P(B\mid A)+P(\bar{A})P(B\mid \bar{A})}=0.2837\]这说明在 10000 个人中真正患肝癌的人有 4 个,但是在剩下的 9996 人中会有 $9996\times0.001=9.996$ 人会在化验单上查出自己阳性,并且在真正患肝癌的 4 人中仅有 $4\times0.99=3.96$ 人能够在化验单上查出自己阳性。如果仅从这 $9.996+3.96=13.956$ 个查出自己阳性的人中看,真正患肝癌的比例约为 28.37%。这是由于未患病的人群基数极大,也会有大量的未患病人群产生假阳性结果,因此导致阳性结果中真正患病的人占比相对较低。
若给疑似患肝癌的人群再次进行复查,此时 $P(A)=0.2837$,这时再用 Bayes 公式计算得
\[P(A\mid B)=\frac{P(AB)}{P(B)}=\frac{P(A)P(B\mid A)}{P(A)P(B\mid A)+P(\bar{A})P(B\mid \bar{A})}=0.9975\]这就大大提高了甲胎蛋白法的准确率了。
保险投保问题
保险公司认为人可以分为两类,一类易出事故,另一类则不易出事故。统计表明一个易出事故者在一年内发生事故的概率为 0.4,而对不易出事故者来说这个概率则减少到 0.2,若假定第一类人占人口的比例为 30%,现有一个新人来投保,那么该人在购买保单后一年内将出事故的概率有多大?再假设一个新投保人在购买保单后一年内出了事故,那么他是易出事故者的概率是多大?
令事件 $A$ 为“投保人一年内出事故”,事件 $B$ 为“投保人为易出事故者”,那么
\[P(A)=P(B)P(A\mid B)+P(\bar{B})P(A\mid \bar{B})=0.26\]另外,由乘法公式与条件概率公式,可得
\[P(B\mid A)=\frac{P(AB)}{P(A)}=\frac{P(B)P(A\mid B)}{P(A)}=0.4615\]多选题蒙题问题
在回答一道多项选择题时,学生或者知道正确答案(记作事件 $K$),或者就猜一个。令 $p$ 表示他知道正确答案的概率,则 $1-p$ 表示猜的概率。假定学生猜中正确答案的概率为 $\frac{1}{m}$,其中 $m$ 就是多项选择题的可选择答案数。那么该学生回答正确(记作事件 $C$)的情况下,他知道正确答案的概率则为
\[\begin{aligned} P(K\mid C)=\frac{P(KC)}{P(C)}&=\frac{P(K)P(C\mid K)}{P(K)P(C\mid K)+P(\bar{K})P(C\mid \bar{K})}\\ &=\frac{p}{p+(1-p)\frac{1}{m}}=\frac{mp}{1+(m-1)p} \end{aligned}\]Bayes 公式还可以用来进行因果推理,有许多“原因”可以造成某一“结果”。现在设我们观察到某一结果,希望推断造成这个结果出现的“原因”。当观察到结果 $A$ 的时候,我们希望反推结果 $A$ 是由原因$B_i$ 造成的概率 $P(B_i\mid A)$。$P(B_i\mid A)$ 为由于代表新近得到的信息 $A$ 之后 $B_i$ 出现的概率。
用一句话总结,Bayes 公式告诉我们,在试验之前对这些假设条件所作的判断(即 $P(B_i)$),可以如何根据试验的结果来进行修正。
使用 Bayes 公式逆推原因
早上你突然发现自己感冒了(记作事件 $A$),其原因可能是:前一天晚上着凉了(记作事件 $B_1$)、其他人感染给你(记作事件 $B_2$)和免疫力下降(记作事件 $B_3$)。已知前一天晚上着凉的概率为 40%,其他人感染给你的概率为 30%,免疫力下降的概率为 30%。并且因为着凉而感冒的概率为 80%,被传染而感冒的概率为 90%,免疫力下降而感冒的概率为 70%。
于是由全概率公式,由于不同原因导致感冒的概率就为
\[P(A)=\sum_{i=1}^{3}P(B_i)P(A\mid B_i)=0.8\]而感冒是由于着凉所引起的概率为
\[P(B_1\mid A)=\frac{P(B_1)P(A\mid B_1)}{P(A)}=0.4\]同理可分别计算出感冒是由于被传染所引起的概率和感冒是由于免疫力下降所引起的概率为
\[P(B_2\mid A)=\frac{P(B_2)P(A\mid B_2)}{P(A)}=0.3375, \quad P(B_3\mid A)=\frac{P(B_3)P(A\mid B_3)}{P(A)}=0.2625\]由此可见,早上引起感冒的原因很有可能是因为前一天晚上着凉而导致的。
出现这种情况是由于 $P(B_i\mid A)\propto P(B_i)P(A\mid B_i)$,而先验概率 $P(B_1)$ 与似然概率 $P(A\mid B_1)$ 在三个原因中都较高,因此后验概率 $P(B_1\mid A)$ 自然也比较高。
失事飞机搜救问题
一架飞机失踪了,推测它等可能地坠落在 3 个区域。令 $1-\beta_i(i=1,2,3)$ 表示飞机坠落在第 $i$ 个区域的情况下,飞机被发现的概率($\beta_i$ 称为忽略概率,表示忽略飞机的概率,通常由该区域的地理和环境条件决定)。求在第 1 个区域没有发现飞机的条件下,飞机坠落在第 $i$ 个区域的条件概率 $(i=1,2,3)$。
令事件 $R_i$ 表示“飞机坠落在第 $i$ 个区域”($i=1,2,3$),事件 $E$ 表示“第 1 个区域没有发现飞机”。我们先来求 $R_1\mid E$ 的概率,此时
\[P(E)=P(R_1)P(E\mid R_1)+P(R_2)P(E\mid R_2)+P(R_3)P(E\mid R_3)=\frac{2}{3}+\frac{1}{3}\beta_1\]于是
\[P(R_1\mid E)=\frac{P(R_1)P(E\mid R_1)}{P(E)}=\frac{\beta_1}{\beta_1+2}\]接着求 $R_2\mid E$ 与 $R_3\mid E$ 的概率:
\[P(R_2\mid E)=\frac{P(R_2)P(E\mid R_1)}{P(E)}=\frac{1}{\beta_1+2}\]同理可得 $P(R_3\mid E)=P(R_2\mid E)=\frac{1}{\beta_1+2}$。
需要指出的是,当搜索了第 1 个区域没有发现飞机时,飞机坠落在第 $j$ 个区域的条件概率会增大($j\ne1$),而落在第 1 个区域的概率会减小,这是一个常识问题:因为既然在第 1 个区域没有发现飞机,当然飞机坠落在该区域的概率会减少,而落在其他区域的概率会增大,而且飞机坠落在第 1 个区域的条件概率是 $\beta_i$ 的递增函数,当增加时增大了飞机坠落在第 1 个区域的条件概率。类似地,$P(R_j\mid E)$是 $\beta_i$ 的递减函数($j\ne1$)。
独立性
独立性的定义
条件概率 $P(A\mid B)$ 一般不等于无条件概率 $P(A)$。也就是说,事件 $B$ 是否发生的信息可能会改变我们对事件 $A$ 出现的把握,只有当 $P(A\mid B)=P(A)$ 时这种信息才不能影响我们对于事件 $A$ 的发生与否的推断,这时就说 $A$ 与 $B$ 是(随机)独立的。
事件 $A$ 的条件概率 $P(A\mid B)$ 与无条件概率 $P(A)$ 的差别在于:事件 $B$ 的发生改变了事件 $A$ 发生的概率,也即事件 $B$ 对事件 $A$ 有某种“影响”。
如果事件 $A$ 与 $B$ 的发生是相互不影响的,则有 $P(A\mid B)=P(A)$ 和 $P(B\mid A)=P(B)$,它们都等价于
\[P(AB)=P(A)P(B)\]另外对 $P(B)=0$ 或者 $P(A)=0$,上式仍然成立。为此,我们用该式作为两个事件相互独立的定义。
两个事件的独立性
设事件 $A$ 与 $B$ 是样本空间 ${\mit\Omega}$ 中的任意两个事件,如果
\[\begin{equation} P(AB)=P(A)P(B) \end{equation}\]成立,则称事件 $A$ 与 $B$ 相互独立(Independence),简称 $A$ 与 $B$ 独立。否则称 $A$ 与 $B$ 不独立或相依(Dependence)。
至于用 $P(AB)=P(A)P(B)$ 作为独立性的定义,而不用 $P(A\mid B)=P(A)$ 的理由如下:
- 独立性是事件之间的一种对称关系,也就是说若事件 $A$ 与 $B$ 独立,那么事件 $B$ 与 $A$ 也必须独立,因此我们需要一个对称性的定义。然而条件概率 $\boldsymbol{P(A\mid B)}$ 是非对称的,它只考虑了已知事件 $B$ 发生下 $A$ 受到的影响,并且 $P(A\mid B)$ 并不总是等于 $P(B\mid A)$;
- 条件概率 $P(A\mid B)$ 要求 $\boldsymbol{P(B)>0}$,在 $P(B)>0$ 的情况下 $P(A\mid B)$ 才有意义。若 $P(B)=0$,则会遇到无法定义事件 $A$ 与 $B$ 的独立性;
- $P(AB)=P(A)P(B)$ 表明,两个独立事件的共同发生的概率仅仅是它们各自发生的概率的乘积,表明它们彼此之间没有任何影响。相比之下,条件概率 $P(A\mid B)=P(A)$ 只描述了在事件 $B$ 已经发生的情况下 $A$ 发生的概率与 $B$ 无关,而无法直观地表达 $A$ 和 $B$ 同时发生的独立性;
- $P(A\mid B)=P(A)$ 可以作为 $P(AB)=P(A)P(B)$ 的推论,即 $$ P(A\mid B)=\frac{P(AB)}{P(B)}=\frac{P(A)P(B)}{P(B)}=P(A) $$
下面是相互独立事件 $A$ 和 $B$ 与它们的对立事件 $\bar{A}$ 和 $\bar{B}$ 之间的关系:
命题 $6$
若事件 $A$ 与 $B$ 独立,则 $A$ 与 $\bar{B} $独立,$\bar{A}$ 与 $B$ 独立,$\bar{A}$ 与 $\bar{B}$ 独立。
证明
由于事件 $A$ 与 $B$ 独立,那么
\[P(AB)=P(A)P(B)\]于是
\[P(A\bar{B})=P(A-B)=P(A)-P(AB)=P(A) [1-P(B)]=P(A)P(\bar{B})\]即事件 $A$ 与 $\bar{B}$ 独立,同理事件 $\bar{A}$ 与 $B$ 也独立。
又由于
\[P(\bar{A}\bar{B})=P(\overline{A\cup B})=1-P(A\cup B)=P(\bar{A})-P(B)P(\bar{A})=P(\bar{A})P(\bar{B})\]即事件 $\bar{A}$ 与 $\bar{B}$ 独立,结论得证。
在实践中,通常 $P(AB)$ 与 $P(A)P(B)$ 的绝对误差不超过 $10^{-3}$ 或者 $10^{-4}$、相对误差不超过 1% 或者 5%,即
\[|P(AB)-P(A)P(B)|\leqslant10^{-4} \quad \text{或者} \quad |P(AB)-P(A)P(B)|\leqslant10^{-3}\]以及
\[\frac{|P(AB)-P(A)P(B)|}{P(AB)}\leqslant1\% \quad \text{或者} \quad \frac{|P(AB)-P(A)P(B)|}{P(AB)}\leqslant5\%\]即认为事件 $A$ 与 $B$ 相互独立,也可以根据实际需要选择合适的显著性水平。
多个事件的独立性
设 $A,B,C$ 是三个任意的事件,若有
\[\begin{equation} \begin{cases} P(AB)=P(A)P(B)\\ P(AC)=P(A)P(C)\\ P(BC)=P(B)P(C) \end{cases} \end{equation}\]则称 $A,B,C$ 两两独立;若还有
\[\begin{equation}\label{eq:三个事件的独立性} P(ABC)=P(A)P(B)P(C) \end{equation}\]则称 $A,B,C$ 相互独立
\eqref{eq:三个事件的独立性}式确保了事件 $A$ 与 $B$ 的任意组合都与 $C$ 独立,事件 $A$ 与 $C$ 的任意组合都与 $B$ 独立,事件 $B$ 与 $C$ 的任意组合都与 $A$ 独立。另外事件 $A,B,C$ 两两独立不能推出事件 $A,B,C$ 相互独立;反过来事件 $A,B,C$ 相互独立也不能推出事件 $A,B,C$ 两两独立!
试验的独立性
试验的独立性
设有两个试验 $E_1$ 和 $E_2$,假如试验 $E_1$ 的任一结果(事件)与试验 $E_2$ 的任一结果(事件)都是相互独立的事件,则称这两个试验相互独立。
例如掷一枚硬币(试验 $E_1$)与掷一颗骰子(试验 $E_2$)是相互独立的试验。
类似地可以定义 $n$ 个试验 $E_1,E_2,\cdots,E_n$ 的相互独立性:如果 $E_1$ 的任一结果、$E_2$ 的任一结果、……、$E_n$ 的任一结果都是相互独立的事件,则称试验 $E_1,E_2,\cdots,E_n$ 相互独立。
如果这几个独立试验还是相同的,则称其为 $n$ 重独立重复试验。如果在 $n$ 重独立重复试验中,每次试验的可能结果为两个:$A$ 或者 $\bar{A}$,则称这种试验为 $n$ 重 Bernoulli 试验。
参考文献
- 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程[M]. 第 3 版. 北京: 高等教育出版社, 2019.
- 李贤平. 概率论基础[M]. 第 3 版. 北京: 高等教育出版社, 2010.
- 王梓坤. 概率论基础及其应用[M]. 北京: 北京师范大学出版社, 2018.
- 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 第 5 版. 北京: 高等教育出版社, 2019.
- Ross S. A First Course in Probability. 9th. Pearson, 2012.
- Feller W. An Introduction to Probability Theory and Its Applications. 3rd. Wiley, 1968.
- Bertsekas D, Tsitsiklis J. Introduction to Probability. 2nd. Athena Scientific, 2008.
- Miller S. The Probability Lifesaver: All the Tools You Need to Understand Chance. Princeton University Press, 2017.
- DeGroot M, Schervish M. Probability and Statistics. 3rd. Addison Wesley, 2001.
-
Experiment 译为“实验”,强调为了测试或验证假设或理论而设计的有控制的研究过程。Trial 译为“试验”,更加强调为实验中的单次尝试或测试,是为实验过程的一部分,指实验中进行的每一个具体操作。 ↩︎
-
Bernoulli J. Ars Conjectandi. 1713. ↩︎
-
Laplace P S. Théorie analytique des probabilités. 1812. ↩︎
-
Von Mises R. Probability, Statistics and Truth. 1939. ↩︎
-
概率(Probability)与似然概率(Likelihood)的区别在于:Probability 是给定参数的情况下预测某个事件发生的可能性;而 Likelihood 是给定数据推测参数的可能性。 ↩︎

